容斥极值问题是行测数量关系中的常见考点，这一考点在资料分析中也有应用。那么今天小编给大家带来的是容斥极值在资料分析中的具体应用：
一、概念引入
容斥极值问题一般求解最小值，这类问题常用的方法是文氏图或者公式法，公式如下：
1.两者容斥极值：(A∩B)min=A+B–I
2.三者容斥极值：(A∩B∩C)min=A+B+C–2I
二、题型特征
题干主体为容斥问题，问题中出现“最大”“最小”“至多”“至少”等字眼
三、例题
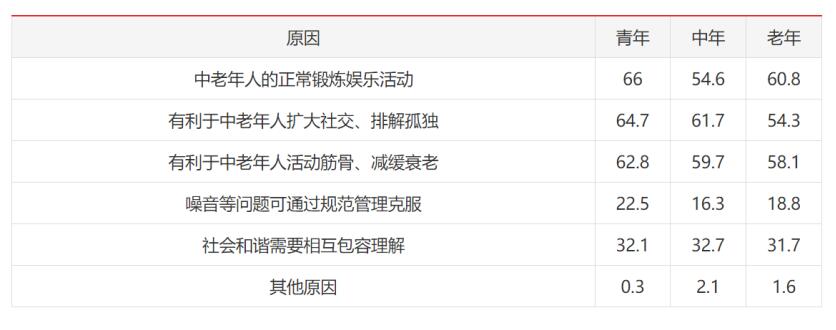
某市统计局在针对噪音扰民的一次调查中，当问及是否支持广场舞活动时，12.8%的受访市民表示无所谓或者不知道，12.0%的受访者回答表示反对，其他为支持者。在支持的市民中，当被问及支持的主要原因(多选)时，不同年龄段受访者的回答如下表。
支持广场舞等活动的受访市民选择各主要原因的比例(%)
问题：此次调查中，在支持广场舞等活动的受访青年市民中，同时选择“中老年人的正常锻炼娱乐活动”和“有利于中老年人扩大社交、排解孤独”的至少有：
A.64.7% B.35.3% C.30.7% D.28.6%
【答案】C。解析：定位至表格材料“中老年人的正常锻炼娱乐活动”和“有利于中老年人扩大社交、排解孤独”所在行;受访青年中“中老年人的正常锻炼娱乐活动”占比为66%，“有利于中老年人扩大社交、排解孤独”的占比为64.7%。问的是“同时选择中老年人的正常锻炼娱乐活动和有利于中老年人扩大社交、排解孤独的至少”的情况，即把选择中老年人的正常锻炼娱乐活动的当作A集合，选择有利于中老年人扩大社交、排解孤独的当作B集合，两者要最少(最少)，即二者尽可能不重合。根据两集合容斥原理：，即，总数U要尽可能的多，最多就是100%，故同时选择“中老年人的正常锻炼娱乐活动”和“有利于中老年人扩大社交、排解孤独”的至少为：66%+64.7%-100%=30.7%。
对于此类问题，需要大家在学习过程中积极概括总结题目特征，匹配相似题目，进行大量练习，熟练使用解题技巧，以便融会贯通。
更多行测技巧与方法扫码获取
行测备考提醒
